競輪の競走得点とは？信頼度は高い？予想のコツとランキング！

この記事では、競輪の競走得点について、

「競走得点ってなに？」

「競走得点を予想に活かすには？」

「競走得点のランキングは？」

といった疑問に回答していきます。

競輪の競走得点とは、出場した競走種目の着により選手に与えられる得点のことです。

出走表に載っているのは平均競走得点で、これは「競走得点の合計/出走回数」で計算されています。

平均競走得点は、選手の実力を判断するのに役立ちますが、注意点もいくつかありますね。

ここからは、競走得点の基礎知識と予想のコツを解説するので、ぜひ最後まで読んでみてください。

競走得点を見れば、選手の実力がわかるんだな！

基本的にはその通りですが、注意点もあるので気を付けましょう。

競輪の競走得点とは？

競輪の競走得点とは、出場した競走種目の着により選手に与えられる得点のことです。

着順が良いほど得点が高くなるので、成績が良い選手にはたくさんの競走得点が与えられますね。

また、出走表には「競走得点の合計/出走回数」で計算された平均競走得点が載っています。

そのため、基本的には、平均競走得点が高い選手ほど車券に絡みやすいと考えていいでしょう。

ここからは、競走得点の基礎知識として、以下の3つを初心者向けに解説していきます。

まずは、競走得点の基礎知識を解説していきます。

競走得点はレースと着順で決まる

出典：KEIRIN.JP

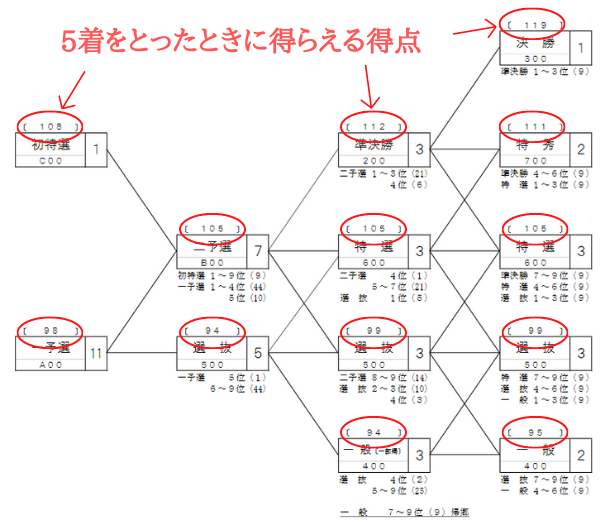
選手に与えられる競走得点は、出場したレースの種類とその着順によって決まります。

具体的には、グレードが高いレースや勝ち上がった後のレースでは得点が高くなりますね。

例えば、G1のほうがF1よりも得点が高く、決勝のほうが予選よりも得点が高いです。

また、着順が良いほど得点が高くなるので、1着のほうが9着よりも得点が高くなります。

つまり、レベルの高いレースで好成績な選手ほど、得られる競走得点は多くなるわけですね。

同じ1着でも、レベルの高いレースのほうが得られる得点は多いぜ！

計算方法は「競走得点の合計/出走回数」

出典：KEIRIN.JP

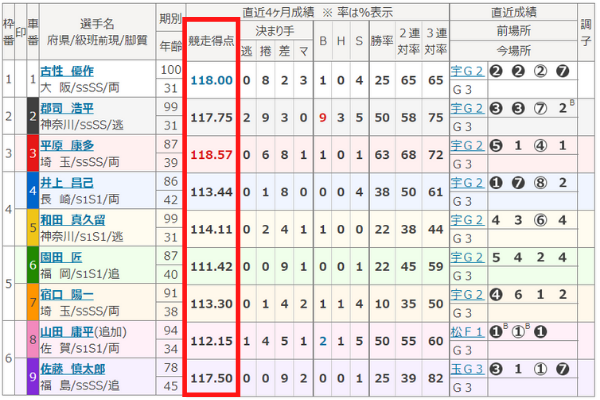
競輪の出走表には「競走得点の合計/出走回数」で計算された平均競走得点が載っています。

先ほども解説しましたが、成績が良い選手ほど、得られる競走得点は多くなりますね。

そのため、平均競走得点が高い選手ほど、これまでの成績が良い選手ということになります。

これまでの成績が良い選手なら、そのレースでも活躍してくれる可能性が高いでしょう。

ちなみに、平均競走得点は言いにくいので、簡単のために競走得点と呼ばれることもあります。

この記事でも、今後は「競走得点=平均競走得点」として扱っていきますね。

競走得点をもとに級班が決まる

出典：KEIRIN.JP

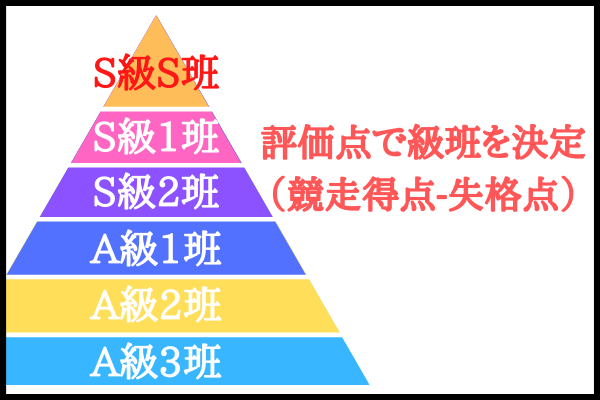
競輪では、毎年2回、選手の評価点によって級班というグループ分けが行われます。

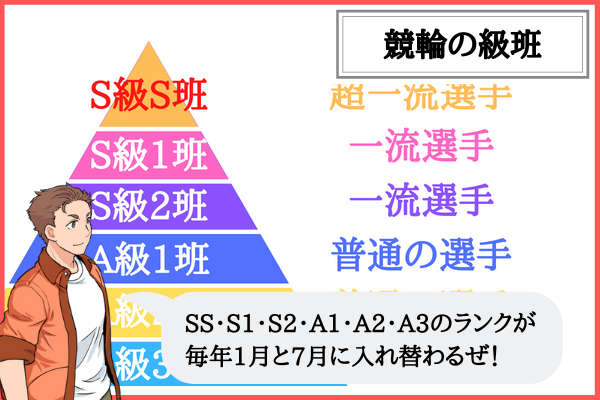
級班は、上から順番にS級S班、S級1班、S級2班、A級1班、A級2班、A級3班の6種類があります。

評価点は「競走得点-失格点」で計算され、審査期間は前期が1～6月、後期が7～12月です。

このことから、競走得点が高い選手ほど上の級班に所属できることになります。

級班が上がれば、出場できるレースのグレードが上がり、賞金を稼ぎやすくなりますね。

級班ごとに定員が決まってるから、ボーダーは期ごとに変わるな！

競走得点が低すぎるとクビになる

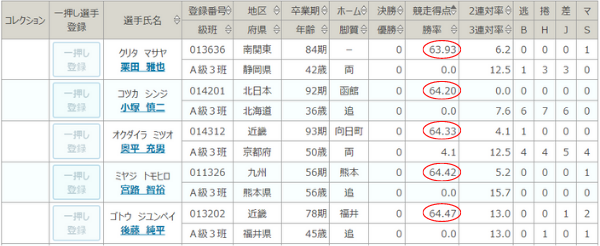
競輪には、競走得点が低すぎる選手をクビにして、選手登録を抹消する代謝制度があります。

成績の審査期間は前期が1～6月、後期が7～12月で、代謝は6月と12月に行われますね。

このとき、男子選手の成績下位30名と、女子選手の成績下位3名がクビになります。

代謝の対象には細かい条件がありますが、競走得点が低い選手は対象になりやすいです。

また、他の選手との比較なので「〇点以上なら大丈夫」というボーダーがないのが怖いですね。

競走得点が低すぎる選手は、6月と12月は選手生命を賭けた勝負駆けになります。

競輪の競走得点を予想に活かすコツは？

競輪の競走得点は、選手の実力を判断するときに参考になるデータです。

基本的には、競走得点が高い選手ほど強く、競走得点が低い選手ほど弱いと考えられます。

しかし、競走得点だけを使って車券を買っても、的中率はなかなか上がらないでしょう。

競走得点だけでは選手の実力は判断できませんし、競輪にはチーム戦の要素もあるからです。

ここからは、競走得点の注意点と予想のコツとして、以下の3つを解説していきます。

予想のコツをマスターして、的中率アップにつなげましょう。

8点差以上は明確な実力差がある

出典：KEIRIN.JP

競走得点を予想に活かすコツの1つ目は、8点差以上は明確な実力差があると考えることです。

これは、競走得点は、着順が1つ変わるごとに2点の差がつくからですね。

そのため、競走得点が8点以上違うと、平均着順が4着以上は違うことが多くなります。

例えば、2022年4月7日の平塚G3の初日特選では、着順ごとの競走得点はこのようになっていました。

このようなレースで2着をとることが多い選手は、競走得点が114点になります。

一方、このようなレースで6着をとることが多い選手は、競走得点が106点になりますね。

106点の選手が114点の選手に勝つには、普段より4名も多く抜かさなければいけません。

これは現実的にかなり厳しいことであり、106点の選手が基本的には負けるでしょう。

予想するときは競走得点を比べて、8点差以上なら明確な実力差があると考えてみてください。

競走得点が8点以上低い選手は、車券に絡みにくいってことだな！

逆に、競走得点の差が4点以内なら逆転の余地がありますね。

勝率や2・3連対率と合わせて考える

出典：KEIRIN.JP

競走得点を予想に活かすコツの1つ目は、勝率や2・3連対率と合わせて考えることです。

これは、競走得点だけでは、選手の実力を正確には判断できないからですね。

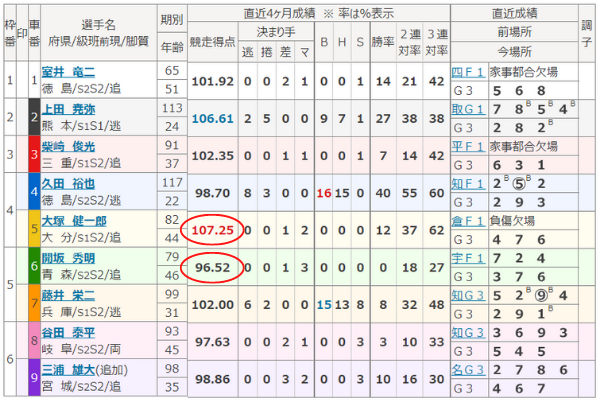
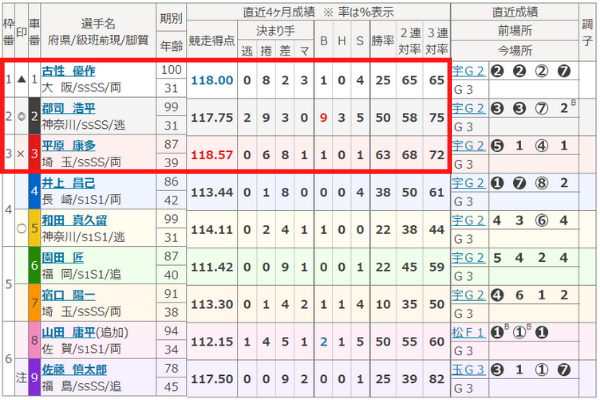
例えば「古性優作」選手、「郡司浩平」選手、「平原康多」選手のデータを比べてみましょう。

下の表では、2着率を「2連対率-勝率」、3着率を「3連対率-2連対率」で計算しています。

敬称略

この3名の競走得点を比べると、平原選手、古性選手、郡司選手の順番に高くなっています。

次に、勝率を比べると、平原選手、郡司選手、古性選手の順番に高くなっていますね。

このことから、平原選手は、1着をとることによって、競走得点を稼いでいると考えられます。

ただし、2・3着率は低いので、1着をとれないときは着外になることが多いのでしょう。

平原選手を買うときは、1着だけを買っておけば良さそうだな！

一方、2着率を比べると、古性選手、郡司選手、平原選手の順番に高くなっていますね。

そのため、古性選手は、2着をとることによって、競走得点を稼いでいると考えられるでしょう。

また、競走得点は、勝ち上がった後のレースのほうがもらえる得点が多くなります。

このことから、古性選手は、決勝・準決勝への勝ち上がりが上手いとも考えられそうです。

古性選手を買うときは、勝ち上がりのかかった2着を買いましょう。

最後に、3着率を比べると、郡司選手、平原選手、古性選手の順番に高くなっています。

郡司選手は3名のなかで3連対率が最も高いので、車券に最も絡みやすい選手と言えそうですね。

このように、競走得点が同じように高い選手でも、とりやすい着順は違っています。

予想するときは、競走得点だけでなく、勝率や2・3連対率と合わせて考えてみてください。

郡司選手を買うときは、1～3着まで手広く買うのが良さそうだな！

ライン戦での着順の逆転を考える

出典：KEIRIN.JP

競走得点を予想に活かすコツの3つ目は、ライン戦での着順の逆転を考えることです。

なぜなら、競輪では、レースの途中まではラインを組んでチーム戦が行われるからですね。

ラインが強ければ、競走得点の低い選手でも車券に絡んでくることがあります。

例えば、174ラインが逃げ、826ラインと935ラインが捲りを狙うレースを考えてみましょう。

このとき、1～9番車の選手の競走得点が、下の表のようになっていたと仮定しますね。

もしも、個人の競走得点だけで勝負が決まるなら、1番車か3番車が1着をとるでしょう。

また、2・3着は2・6・8番車が有力で、4・5・7・9番車は着外になりそうですね。

しかし、競輪はライン戦があるので、単純にこのような結果になるとは限らないのです。

競輪のレースは、チーム戦と個人戦の両方があるから面白いですね。

まず、先ほどの表から、ラインごとの競走得点をまとめると、

• 174ライン・・・118・112・112
• 826ライン・・・114・114・114
• 935ライン・・・112・118・112

となります。

174ラインが逃げを狙うのであれば、1番車の強い選手がラインを引っ張って先行します。

このとき、7・4番車は、1番車に付いて行くだけで簡単に2・3着をとれるのです。

そのため、このレースでは、7・4番車は競走得点以上に車券に絡みやすいと言えます。

ただし、1番車と7・4番車の間に実力差がありすぎると、付いて行けずに千切れてしまいますね。

同じ府県や地区のラインは、ラインの結束が強くなるな！

次に、935ラインは捲りを狙うのですが、9番車は1番車の間には実力差があります。

すると、9番車は1番車を捲り切れずに、捲りが不発に終わってしまうことがあるのです。

このとき、番手の3番車は自力がなければ、9番車と一緒に着外になってしまいます。

そのため、3番車は競走得点が高いわりには車券に絡みにくいと言えるでしょう。

個人の競走得点だけではなく、ライン戦での展開予想をすることが重要なわけですね。

ライン戦をマスターして、的中率アップを目指しましょう。

競輪の競走得点のランキングは？

競輪では、レベルの高いレースで好成績な選手ほど、競走得点が高くなります。

では、競走得点の高い選手は、実際にはどの選手なのでしょうか？

今回は、この記事を書いている2022年4月7日時点でのランキングをまとめました。

このランキングに載っている選手は、2022年のレースで活躍が期待できます。

また、最新のランキングを知りたいときは、KEIRIN.JPの検索/資料室を活用しましょう。

ランキングは、男子選手と女子選手にわけて作成しました。

男子選手の競走得点ランキング

敬称略・2022年4月7日時点

男子選手のランキング上位10名は、S級S班の選手が6名、S級1班の選手が4名でした。

S級S班の選手は、2021年の競輪グランプリに出場しただけあって、さすがに強いですね。

一方、S級1班の選手は、最近調子を上げてきたことになるので、活躍に期待できます。

特に、脇本選手や新田選手は、2021年は競輪のレースにはほとんど出場していませんでした。

しかし、競走得点上位に入っているところを見ると、2022年はS級S班に復活しそうですね。

脇本選手や新田選手は、2021年は東京オリンピックに専念していたな！

ガールズケイリンの競走得点ランキング

敬称略・2022年4月7日時点

女子選手のランキング1位は神奈川県の「佐藤水菜」選手で、競走得点は57.71点でした。

佐藤選手は、2021年は40走のうち1着37回、3着3回の凄い成績を残した選手です。

さらに、特別競輪のアルテミス賞レースとガールズケイリンコレクションも優勝しています。

また、自転車競技にも注力しており、2021年の世界選手権では女子ケイリンで準優勝を決めました。

2022年もここまで7走して1着6回、2着1回なので、今後の活躍にも注目したいところです。

ガールズケイリンは個人戦だから、強い選手が独走しやすいですね。

競走得点の過去最高は131.14

出典：KEIRIN.JP

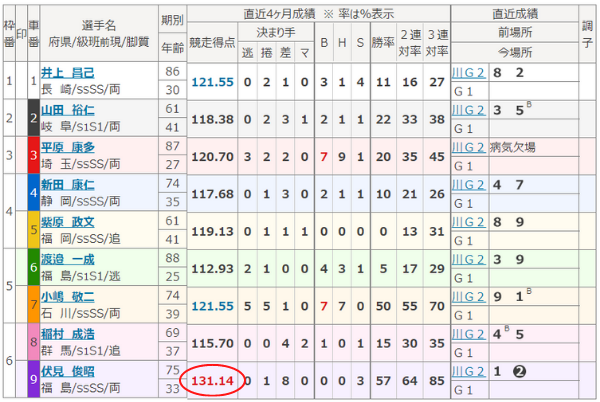
競走得点の過去最高記録を調べたところ「伏見俊昭」選手の名前が出てきました。

上の出走表は、2009年の全日本選抜競輪ですが、伏見選手の競走得点は131.14もありますね。

2番目に高いのが121.55点なので、この時期は伏見選手が圧倒的に強かったようですね。

また、現在のランキング1位「平原康多」選手も118.57点なので、それよりも10点以上高いです。

現在の伏見選手はこの時期ほどの強さはありませんが、出走表で見かけたら注意しましょう。

伏見選手は2022年前期はS級2班だけど、後期はS級1班に復活予定だぜ！

競輪の競走得点｜よくある質問

ここからは、競輪の競走得点についてのよくある質問をまとめました。

気になる疑問があれば、回答を読んで解決しておきましょう。

競走得点の信頼度は低い？当てにならない？

競走得点は選手の成績をもとに計算されるので、信頼度は高いです。

ただし、この記事にも書いたような注意点があるので、予想するときは気を付けましょう。

競走得点に失格は反映される？

選手が失格になっても、競走得点がマイナスされることはありません。

そのレースは出走回数にカウントされず、競走得点の計算には反映されなくなります。

競走得点の級班のボーダーは？

2022年後期の評価点のボーダーは、S級1班が103.85点、S級2班が91.17点でした。

例年通りなら、2023年前期のボーダーもこのくらいの数値になりそうです。

競走得点の代謝のボーダーは？

2022年後期の代謝では、競走得点のボーダーが男子は67.7点前後、女子は44.6点前後になりそうです。

最新の代謝のボーダーについては、競輪明るくない…というサイトにまとめられています。

競輪の競走得点について、細かい部分までわかったぜ！

最後に、この記事をおさらいしましょう。

競輪の競走得点｜まとめ

競輪選手の競走得点についておさらいすると、

の5つがポイントです。

競輪の競走得点は、選手の実力を判断するときに参考になるデータです。

しかし、競走得点だけを使って予想しても、的中率はなかなか上がりません。

選手の実力を判断するときは、勝率や2・3連対率と合わせて考えましょう。

また、選手個人の実力だけでなく、ライン戦の展開予想もしてみてください。

競輪について、もっと知りたいぜ！

初心者向けの記事をまとめたので、よかったら読んでみてください。

おすすめの関連記事